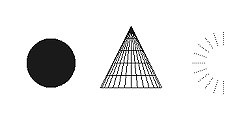| |
||
| |
|
|
| |
||
|
Zum Download des Quellcodes dieser Lektion: Auf das Bild klicken oder hier. Geometrische Primitive
mit GLU a1x2 + a2y2 + a3z2 + a4xy + a5yz + a6xz + a7x + a8y + a9z + a10 = 0 beschrieben werden können. Damit lassen sich verschiedenste Oberflächen annähern [WNDS99]. Um Quadrics benutzen zu können, muss zuerst ein Quadrics-Objekt erzeugt werden. Dies geschieht mit dem Befehl gluNewQuadric(..). Danach werden die Rendering-Attribute für das Quadrics-Objekt festgelegt. So kann über den Befehl gluQuadricDrawStyle(..) bestimmt werden, ob Punkte (GL.GL_POINTS), Linien (GL.GL_LINES) oder gefüllte Polygone (GL.GL_FILL) zur Ausgabe des Objekts benutzt werden sollen. Wenn das Objekt beleuchtet werden soll, müssen die Normalen für das Objekt spezifiziert werden. Dies geschieht mit gluQuadricNormals(..). Dabei kann eine Normale pro Fläche oder pro Vertex erstellt werden. Der Methode wird das erzeugte Quadrics-Objekt übergeben, sowie eine Konstante, mit der sich einstellen lässt, wie die Normalenvektoren erzeugt werden sollen. Standardmässig ist die Einstellung GLU_NONE. In diesem Fall werden keine Normalenvektoren erzeugt, was sinnvoll ist, wenn keine Beleuchtung verwendet wird. Mit der Konstanten GLU_FLAT wird ein Normalenvektor für jede Facette erzeugt. Dies bietet sich für Flat Shading an, während bei Smooth Shading die Konstante GLU_SMOOTH verwendet werden sollte. Auf Beleuchtung wird in Kapitel 4 näher eingegangen. Schließlich muss eine von vier Rendering Routinen aufgerufen werden, um den Typ des Quadrics-Objekts festzulegen. Es können Kugeln, Zylinder, Disks und Partial Disks erzeugt werden. Um eine Kugel zu erzeugen, wird die Methode gluSphere(..) verwendet. Dabei wird das erzeugte Quadrics-Objekt übergeben, der Radius der Kugel, sowie die Feinheit der Unterteilung mit Breiten- und Längengraden (Slices bzw. Stacks). Ein Zylinder kann mit gluCylinder(..) erstellt werden. Es wird der Radius des unteren und des oberen Endes übergeben. Zusätzlich wird die Anzahl der Slices und der Stacks übergeben. Zylinder sind unten und oben offen. Die Methode gluDisk(..) zeichnet eine Scheibe mit einem inneren Radius und einem äusseren Radius. Auch hier kann die Feinheit der Auflösung eingestellt werden und zwar mittels Slices und der Anzahl der konzentrischen Kreise. Es kann mit gluPartialDisk(..) auch nur ein Teil der Scheibe gezeichnet werden. Dazu wird der Methode zusätzlich zu den Parametern von gluDisk(..) noch der Winkel angegeben, bei dem der Scheibenausschnitt beginnen soll und der Winkel, der die Größe des Scheibenausschnitts bestimmt. In folgendem Codebeispiel werden drei Quadricobjekte erzeugt, eine
Kugel, ein Zylinder und ein Scheibenausschnitt. Diese werden mit jeweils mit
verschiedenen Rendering-Attributen erstellt: GLUquadric qobj0 = glu.gluNewQuadric(); gl.glTranslatef(-1, 0, 0); //Kugel gl.glTranslatef(1.3f, -0.4f, 0); //Zylinder gl.glRotatef(90, 1, 0, 0); //Scheibenausschnitt
Geometrische Primitive mit GLUT Eine andere Möglichkeit geometrische Primitive zu erstellen, bietet das OpenGL Utility Toolkit, kurz GLUT. Da OpenGL plattformunabhängig konzipiert wurde, stellt es keine Routinen zur Verfügung, um mit der graphischen Oberfläche des jeweiligen Betriebssystems interagieren zu können. Auch Benutzereingaben können durch reines OpenGL nicht verarbeitet werden. Deshalb wurde GLUT entwickelt, um die wichtigsten Routinen zur Fensterverwaltung und zur Interaktion mit dem Benutzer zur Verfügung zu stellen. Diese Funktionen sind für JOGL nicht relevant, da die entsprechenden Methoden mit AWT und Swing implementiert werden. Allerdings enthält GLUT auch Routinen zur Erzeugung von geometrischen Primitiven, auf die nun näher eingegangen werden soll. Um auf GLUT-Routinen zugreifen zu können, muss immer die Bibliothek net.java.games.jogl.util.GLUT importiert werden. Folgende dreidimensionale Objekte lassen sich mit GLUT erzeugen, und zwar entweder in der Gitternetzdarstellung oder als ausgefüllte Körper: Kegel, Würfel, Dodekaeder, Ikosaeder, Oktaeder, Kugel, Tetraeder und Torus. Bei Kugeln und Kegeln wird immer ein GLU Objekt übergeben, da die Funktionen glutSolidSphere(..), glutWireSphere(..), glutSolidCone(..) und glutWireCone(..) nichts anderes machen als die entsprechenden GLU-Methode aufzurufen, um die Objekte zu erzeugen. Bis auf die übergebene GLU-Instanz sind die Parameter deshalb gleich mit den Parametern der GLU-Routinen. Bei der Erzeugung von Mehrecken wird die entsprechende Methode mit einem GL-Objekt als Parameter aufgerufen. Die Größe muss die entsprechenden Skalierungsmethode angepasst werden. Als Beispiel seien die Methoden glutSolidIcosahedron(..) bzw. glutWireIcosahedron(..) genannt. Um einen Torus zu erzeugen, wird entweder glutSolidTorus(..) oder
glutWireTorus(..) eine GL-Instanz, der innere und der äussere
Radius sowie die Feinheit der Unterteilung in Seiten und Ringe als
Parameter übergeben. Mit folgenden Codezeilen werden vier geometrische Primitive, Ikosaeder, Torus, Kugel und Würfel, erstellt und die beiden Möglichkeiten der Darstellung demonstriert: //Icosaeder in Gitternetzdarstellung //Rücksetzen auf Einheitsmatrix //Torus in Gitternetzdarstellung //Kugel ausgefüllt //Würfel ausgefüllt
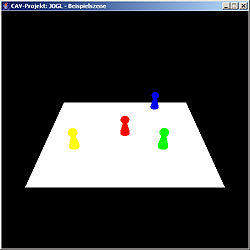
Für unser Spiel werden die Figuren ebenfalls mit GLU-Primitiven gezeichnet. Wir benötigen dafür eine Kugel und zwei Zylinder. Die Erzeugung lagern wir in die Methode drawFigure(..) aus, der außer einer Instanz von GL und einer von GLU ausserdem noch die Position im Raum übergeben wird. Um eine Figur zeichnen zu lassen, rufen wir dann einfach in der display-Methode drawFigure(..) auf, beispielsweise: gl.glColor3f(1f, 0f, 0f); gl.glColor3f(1f, 1f, 0f); gl.glColor3f(0f, 0f, 1f); gl.glColor3f(0f, 1f, 0f); gl.glColor3f(1f, 1f, 1f); Da wir noch nicht mit Materialien und Lichtern arbeiten, benutzen
wir glColor3f(..) um den Figuren unterschiedliche Farben zuzuordnen.
public void drawFigure(GL gl, GLU glu, float x, float z) gl.glTranslated(x, 0, z); glu.gluQuadricDrawStyle(qobj, GLU.GLU_FILL); gl.glRotated(90, 1, 0, 0); gl.glTranslated(0, 0, 1.2f); gl.glPopMatrix(); Wir benutzen dabei glPushMatrix(), um die aktuelle Matrix zu speichern. Danach können wir die Transformationen zum Anordnen der einzelnen Teile unserer Spielfigur vornehmen. Damit wir die danach zu zeichnenden Elemente der Szene nicht durch diese Transformationen manipulieren, versetzen wir die Modelview-Matrix mit glPopMatrix wieder in den Zustand, den sie vor dem Zeichen der Spielfigur innehatte. |
||